正四角錐の体積(底辺と高さから) 答えを知れて良かったが、途中式が分からないので、あまり勉強にはならなかった。 a=8,h=3にすると体積がになります。 (14桁の場合) 正しくは、64です。 修正お願いいたします。 失礼致しました。 ご指摘ありがとうございます。 修正致し RSQUPYRAMIDカスタムワークシート関数群は、正四角錐の体積や表面積などを計算します。 正四角錐とは、正方形と合同な4つの三角形で構成されたピラミッド型です。 RSQUPYRAMIDカスタムワークシート関数群には、下記の関数が含まれます。 ワークシート関数だけで (VBAを使用せずに)同じことをしたい場合は コチラ の記事を参照して下さい。 関数名 機能 関数正四角錐の高さを含む直角三角形に注目、三平方の定理から高さを求める。 ②で求めた高さを用いて、体積の公式に当てはめて計算する。 練習問題に挑戦しよう!問題 次の正四角錐の体積を求めなさい。 解説&答えはこちら

中学3年の数学 動画 相似と体積 基本編の問題 19ch
正四角錐 体積 高さ
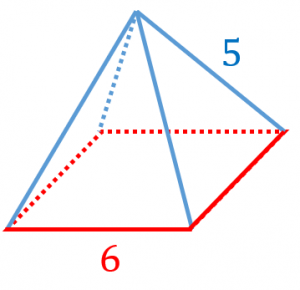
正四角錐 体積 高さ-5515 先がとんがっている立体の体積の計算は「底面積×高さ×1/3」になる って覚えておけば問題ないよ。 だから例題の正四角錐の体積は、 6×6×8×1/3 = 96cm³ になるんだ。 おめでとう!これで正四角錐の体積を計算できたね^^ まとめ:正四角錐の体積の求め方も大丈夫!5919 正方形abcdの対角線の交点をhとする。 pacはpa=pcの二等辺三角形なのでph⊥acである。 ac=6 2 よりah = 3 2 、pa=3 6 三平方の定理より ph 2 18 = 54 ph = 6 体積を求める。 正方形abcd = 6×6 = 36 pabcdの体積は 36×6÷3=72 pabの面積を求める。 pa=pb=3 6 、ab=6なので ∠apb=θとす




四角錐 Wikiwand
体積 一辺を とすると = ;正四角錐の体積の公式を3ステップで解説します。求め方がよくわからないときに参考にしてみてください。 Step1 底面積を計算するっ! まずは正四角錐の底面積を求めてみよう。 正四角錐の底面は「正方形」だよね?? 正方形の面積を「1辺×1 体積は 0 cm 3 表面積は 0 cm 2 ※√2= ※√3=
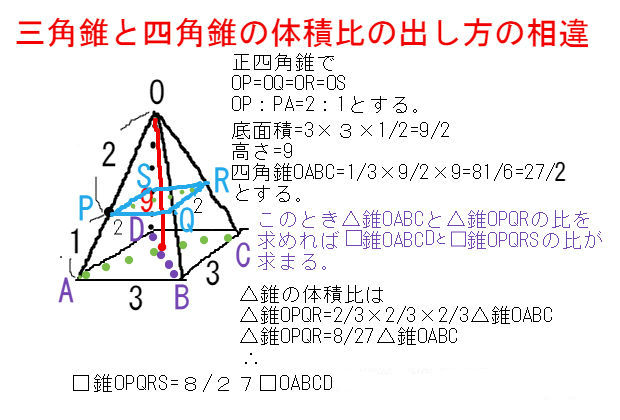
6321 三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1 ×底面積×高さ 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h の導出を紹介します。正四角錐A-BCDE の 体積 を V とします。 図2で、 三角錐B-APQ と B-ACE の 比 を求めましょう。 底面の比 は △APQ : △ACE = 1:4 、 高さ は 共通 、よって 体積比 は 1:4 。五角錐(ごかくすい、英 pentagonal pyramid )とは、底面が五角形の角錐である。 特に底面が正五角形で、頭頂点から底面に下ろした垂線が底面の中心で交わるものを正五角錐といい、その側面は二等辺三角形である。 正五角錐の内、側面が正三角形のものは2番目のジョンソンの立体である。
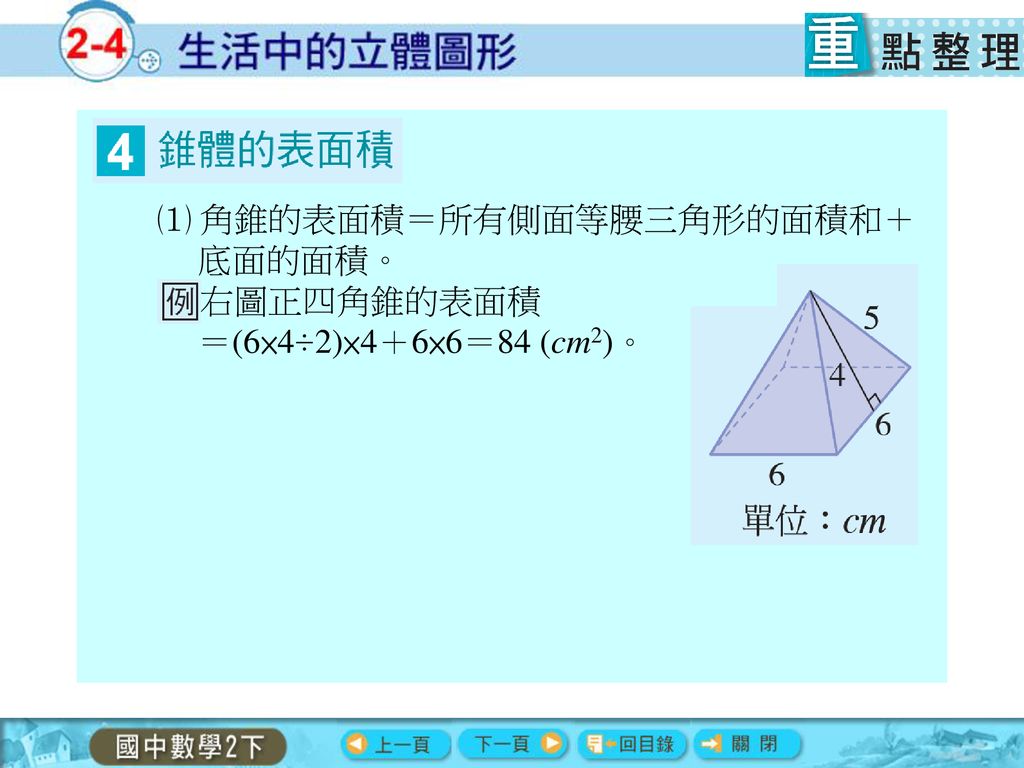
(正五角柱の体積S):(五角錐の体積T)= 5 a : a 3 2 = 5 : 3 2 =15:2 問題 右の図のように,立方体の底面の各辺の中点と,この面と向かい 合う面の対角線の交点を結ぶと正四角錐ができる。このとき,正四 角錐の体積は,立方体の体積の何倍になるかを 四角錐 体積 公式 5 底面が正方形で、正四角錐なので、底面の対角線の交点上に高さとなる垂線は下りてきます。, (2) どなたか、簡単な説明方法を教えてください。 ちなみに負かけ正、正かけ負の計算は理解できています。 この問題の円錐の表面積を底面が1辺8cmの正方形で、他の辺が9cmの正四角錐OABCDの体積を求めよ。 A B C D O 9cm 8cm 底面が1辺12cmの正方形で、他の辺が10cmの



第87問の解答




正四稜柱 上 下底面都是正方形 且側棱垂直於底面的稜柱叫做正四稜柱 正四 百科知識中文網
正四角錐の体積は3つのステップで計算できちゃうんだ。 例題をときながらみていこう! 底辺の1辺の長さが6 cm、高さが8 cmの正四角錐の体積を求めてください。 Step1 四角錐台の体積 斜切円柱の体積正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積141 次の正四角錐の体積を求めなさい。 正四角錐の体積を求めるためには $$(体積)=(底面積)\times \color{red}{(高さ)}\times \frac{1}{3}$$




正四角錐の表面積と体積の求め方を教えてください Clear



この写真の正四角錐の高さの求め方教えてください 四角錐の体積の公式 Yahoo 知恵袋
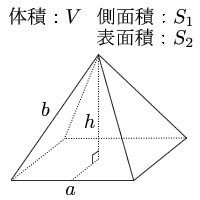
正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積四角錐を平面で切った立体の体積比は (向かい合う1組の辺比の積) x (もう1組の辺比の平均) になるようです でも、これは底面が平行四辺形以上の特殊な場合でないと使えないし、そもそも四角錐を縦に切る作業がわかってしまえば面倒でも 正四角錐の体積 = 64×7÷3 = 448 3 cm 3 つぎの立体のの体積正四角錐柱(せいしかくすいちゅう、elongated square pyramid)とは、8番目のジョンソンの立体で、正六面体の内の1つの底面に四角錐をつけたものである。 性質 表面積 一辺を とすると = ();




直撃 中学入試 第135回 筑波大附属中 立体 正四角錐の切断 北辰塾 情報局




高中 B4 1 1 兩面角 四角錐 尹正數學 Youtube
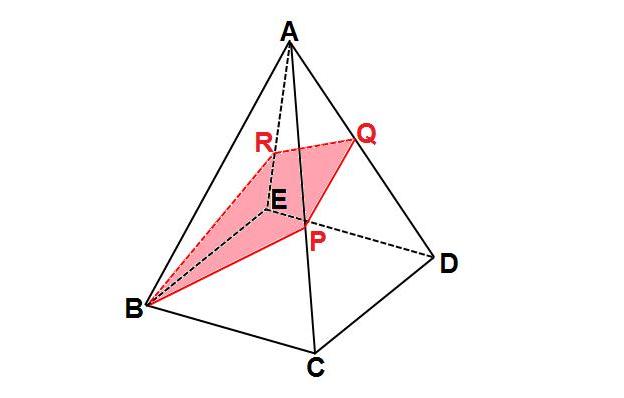
正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積左図は、 底面 が 正方形 で、 OA = OB = OC = OD 、 体積 が 144cm3 である 正四角錐O -ABCD を表しています。 いま、3点 Q 、 R 、 S を通る 平面 でこの 正四角錐 を 切断 します。 (正四角錐iabcd) (正四角錐iefgh) = 1/3 × ( 66) × 4^2 – 1/3 ×6 × 2^2 = 64 – 8 = 56cm^3 になる。 おめでとう! これで台形の体積、、じゃなくて、 正四角錐台の体積を計算できたね!! まとめ:台形の体積の求め方は「上 – 下」!
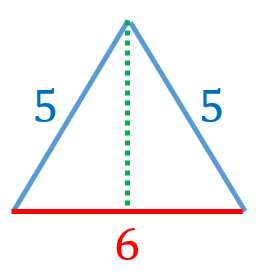



正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
四角錐・四面体・球 トップ・バッターは,1991 年東大・文科の,正四角錐体と球との共通部分の体積を考え る問題です. 6・1正四角錐Vに対し,その底面上に中心をもち,そのすべての辺と接する 四角錐の体積・展開図・塗り分け(21都立青山・改題) 空間幾何 場合の数・確率 小学生~中2生対応可能 都立 (神奈川県立)入試問題 「 三平方の定理 」を試験範囲から除外した今年の入試問題なので、小学生にも解ける内容になっています。 「展開図 正多面体が5種類しかないことの2通りの証明 球面上の三角形の面積と内角の和 球の体積と表面積を積分で証明 四平方の定理(図形の面積と正射影) 四面体の重心の存在証明と応用例 球面上の多角形の面積と美しい応用



Http Tea Ymsh Tp Edu Tw Gallery 157 157 5194 Pdf



Http Www Goodschool Com Tw Doc Www Goodschool Com Tw Concept Pdf
A B C D O 15cm 12cm 底面が1辺12cmの正方形で、他の辺が15cmの正四角錐OABCDの体積を求めよ。 A B C D O 15cm 12cm O A C 15cm 15cm D A B C 12cm 12cm 点O,A,Cを通る平面で切断する。 切断面の OACは二等辺三角形 《四角錐の体積の求め方》 (底面は一辺が5cmの正方形) 四角錐の体積=底面積×高さ× 1 3 なので 求める四角錐の体積=5×5×15× 1 3 =125(cm³)立体の体積、表面積 問題 ・・・ (む) は難しい問題です。 1 右図の四角錐の底面は1辺の長さ6 (cm)の正方形,側面は等しい辺の長さが2√7 (cm)の二等辺三角形です。 この四角錐の体積は (cm 3 ) ア= イ= この四角錐の表面積は (cm2) ウ= エ= オ= 2 右図は1辺の
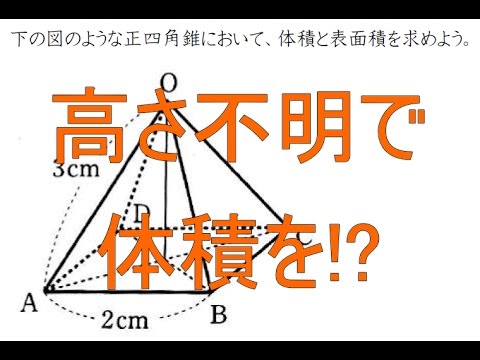



正四角錐と三平方の定理 中学3年数学 Youtube



Www Shs Edu Tw Works Essay 19 10 Pdf
要点四角錐,三角錐,円錐の体積 三角錐,四角錐,円錐の体積 V は,それがちょうど入る四角柱,三角柱,円柱の体積の です. 特に,円錐については,底面の半径が r であるとき,底面積が S=πr 2 と書けるから と書くこともできます.正四角錐の体積 = 64×7÷3 = 448 3 cm 3 つぎの立体のの体積を求めよ。 母線の長さ 13cm, 底面の半径5cmの円錐 母線の長さ 6cm, 底面の半径4cmの円錐 母線の長さ 7cm, 底面の半径2cmの円錐 底面が1辺12cmの正方形で、他の辺が11cmの正四角錐 底面が1辺4cmの正方形で、他の辺が3cmの正四角錐体積4 (発展) 図のような底面が直角三角形 (∠ABC=90°)の三角柱がある。 AB=3㎝、BC=4㎝、CA=5㎝、AD=10㎝である。 この三角柱の辺BE上にBP=6㎝となる点Pをとり、点A,P,Fを通る平面でこの立体を2つに分けてできるそれぞれの立体の体積を求めよ。 図の直方体は AB




Struggling With Problems Like These Think It S 3d Geometry How Can I Get Better At Solving These Type Of Problems Learnmath
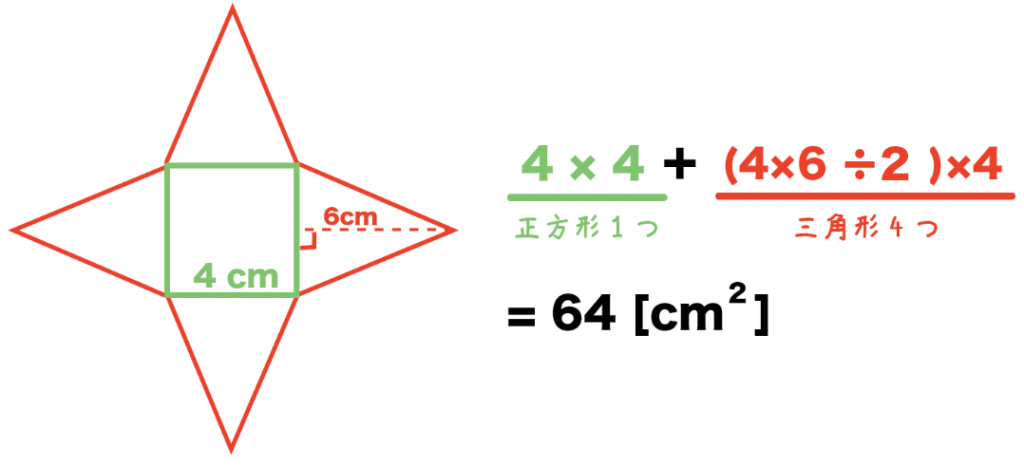



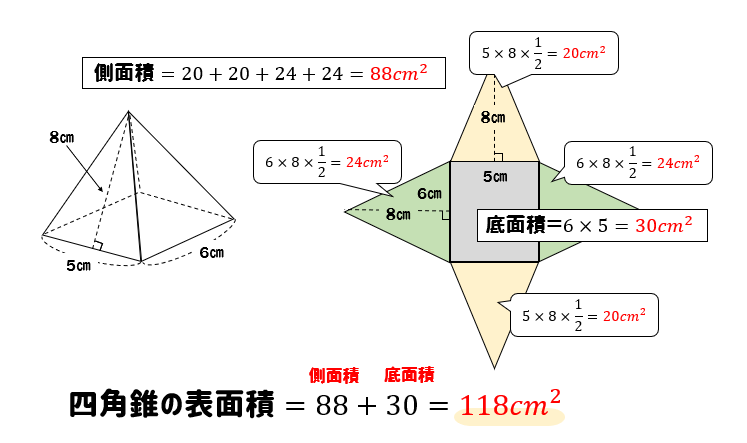
簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
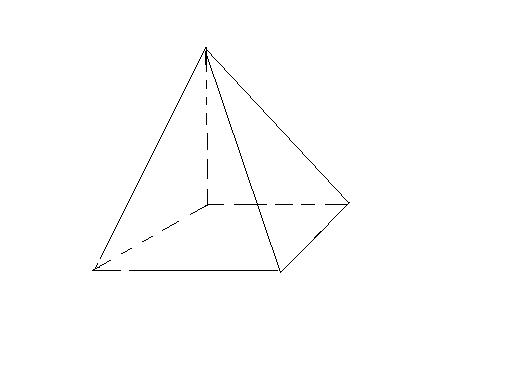
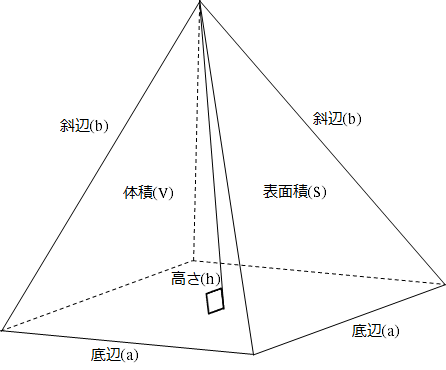
正四角錐の底面が正四角形です。底辺の長さ (a) が等しいです。縦辺の長さ (b) も同等です。側面が二等辺の三角形です。正角錐の高さの基点が底面の中心と一致します (O) 。 角錐の側の面が側面を形成します。正四角錐の場合は、側面が二等辺の三角形です。三角錐でも良いが、すべての面が合同な正三角形なので正四面体が最も適切である。 (2) 正四面体acfhの体積を直接出すことは無理なので、 立方体から、いらない部分を引き算して求める。 いらない部分は全て同じ形の三角錐である。下図のような正四角錐oabcdがあり、その辺の長さはすべて6cmです。 oaを2:1に内分する点をpとします。 qはoc上を動きます。 平面bpqとodとの交点をrとします。 問題1 oq:qc=1:2の時、四角錐opbqrの体積を求めてください 問題2




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




灘 正四角錐の切り口の面積 ジーニアス 中学受験専門塾




如何求金字塔形物體 正四角錐 的體積 中學數學課 隨意窩xuite日誌



Twsf Ntsec Gov Tw Activity Race 1 60 Pdf Nphsf Pdf 504



1




四角錐 Wikiwand




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun




正四角錐の体積を求める問題 図のような正四角錐pabcdにおいて 頂点p Okwave
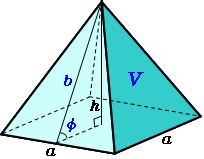



正四角錐の体積 底辺と高さから 高精度計算サイト




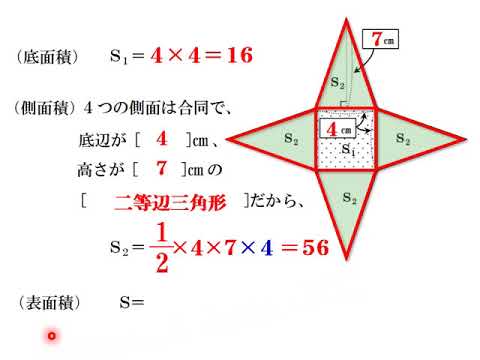
9 如圖 九 是一個正四角錐 其底面正方形的邊長為6公分 側面等腰三角形的腰長為5公分 求此四角錐的表面積 9




中学3年の数学 動画 相似と体積 基本編の問題 19ch




四角錐 四角錐通常指的是一個底面為四邊形的錐體 種類有長方錐 正四角錐和 百科知識中文網



角錐表面積的計算實例 Live 多媒體數學觀念典online
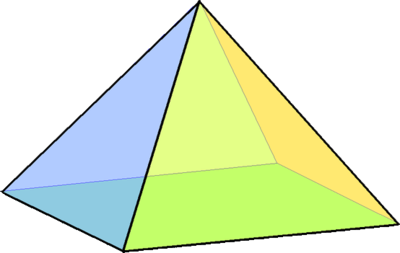



五面體wiki Thereaderwiki



Mathematics 立体の切断 高校入試に出る難しい問題 働きアリ




高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ



如何求金字塔形物體 正四角錐 的體積 中學數學課 隨意窩xuite日誌
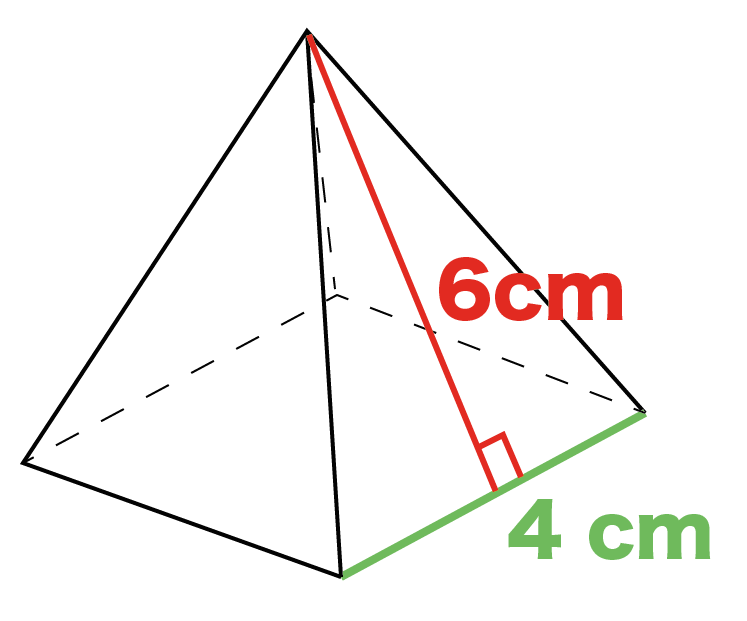



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




國立蘭陽女中數學教師陳敏晧國立清華大學歷史所博士班 Ppt Download



Www Shs Edu Tw Works Essay 19 10 Pdf



Http Jendo Org Files 6year E6 95 99 E5 Ad B8 E8 87 E6 Ba 90 E6 95 B8 E5 Ad B8 E5 87 E4 B8 E8 92 E9 8c 90 A113 Pdf




四角錐台の体積 高精度計算サイト




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




100以上四角錐体積公式 ユニークな壁紙サイトhd



2
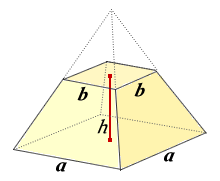



みんなの知識 ちょっと便利帳 正四角錐台の体積を計算する




立体の体積と表面積 Ict教材eboard イーボード




正四角錐の外接球 数学カフェjr



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ




四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後




無料ダウンロード四角錐表面積公式 最高のぬりえ
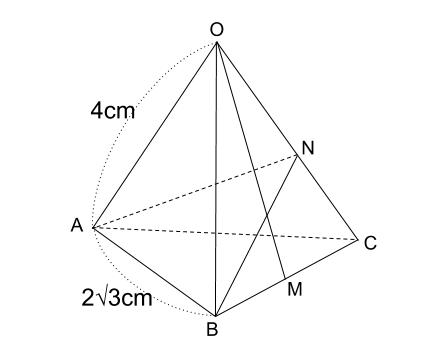



正四角錐の良問 その1 中学数学の無料オンライン学習サイトchu Su




空間向量 正四角錐例題 Youtube



7章1節09 正四角錐の体積 中村 翔




角錐體角椎體兩面角之於弦值 Gquhm



Studydoctor正四角錐と三平方の定理 中学3年数学 Studydoctor




2 1空間慨念



8 1 6cm 5c1n Descubre Como Resolverlo En Qanda




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
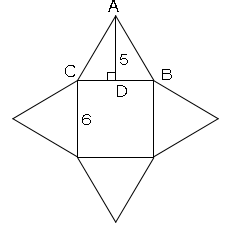



正四角錐の体積の問題 数学の要点まとめ 練習問題一覧




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成



四稜錐 體積公式 體積公式推導 中文百科全書




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




Ppt 四角錐の体積 積分学まで待たねばならないか Powerpoint Presentation Id 7703




角錐 円錐の体積と表面積の公式 数学fun




三平方の定理でこの正四角錐の体積を求めるのですが Clear




つぎの正四角錐の側面積 高さ 体積を求めてください 三平方の定理です Clear




最高正四角錐体積公式 最高のぬりえ



Www Sdime Ntnu Edu Tw Uploads Asset Data 5dfad41c E9 96 B1 E8 Ae 80 E4 B9 9d E4 B8 8b E7 Ac Ac E4 Ba 8c E7 Ab A0 E5 85 A8 Pdf




角錐表面積的計算實例 Live 多媒體數學觀念典online



超難問 正四角錐の切断面の面積と切断立体の体積 中学数学 理科 寺子屋塾の復習サイト



四角錐に関する問題




正四面积体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



正四角錐 底辺と高さ 体積 表面積の計算 計算サイト




四角錐 维基百科 自由的百科全书



Math 立体の切断 高校入試に出る難しい問題 働きアリ The 2nd



1 1 負數與數線



美しい正四角錐体積



Http Blog Whsh Tc Edu Tw Math Wp Content Uploads Sites 5 16 03 E9 Ab 98 E4 B8 Ad E6 95 B8 E5 Ad B8 E7 91 E5 Ae E7 95 B0 E5 8c 96 E8 95 E9 87 8f E2 80 E5 Ad B8 E5 B9 B4 E5 Ba A6 E9 Ab 98 E4 Ba 8c E4 B8 8b E7 Ac Ac1 E6 Ac A1 E5 Ae 9a E6 9c 9f E8 80 E8 E5 85 A8 E6 96 87 Pdf




どうして1 3なの 錐の体積の公式の求め方 まなべーと



1 Boy的聲音問 Ppt Download




三平方の定理を利用して四角すい 円すいの体積を求める 無料で使える中学学習プリント



Www Shs Edu Tw Works Essay 19 10 Pdf




四角錐の体積の求め方 公式 小学生 中学生の勉強



正四角錐の体積は 立方体の体積の何倍になるのでしょうか という問題がで Yahoo 知恵袋




正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学



Images Of 四角錐 Japaneseclass Jp



1




Ppt 除了平面圖形以外 像下列這些在生活中常見物體的形狀都是立體圖形 Powerpoint Presentation Id




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ



第57問の解答



三角錐と四角錐の体積比計算方法の違い 中学数学 理科 寺子屋塾の復習サイト




1 Vcm3 V A Descubre Como Resolverlo En Qanda




50 素晴らしい角錐体積公式 ページを着色するだけ



1



Excel関数 正四角錐 ピラミッド型 の体積や表面積を計算するrsqpyramidカスタムワークシート関数群 黒い箱の中
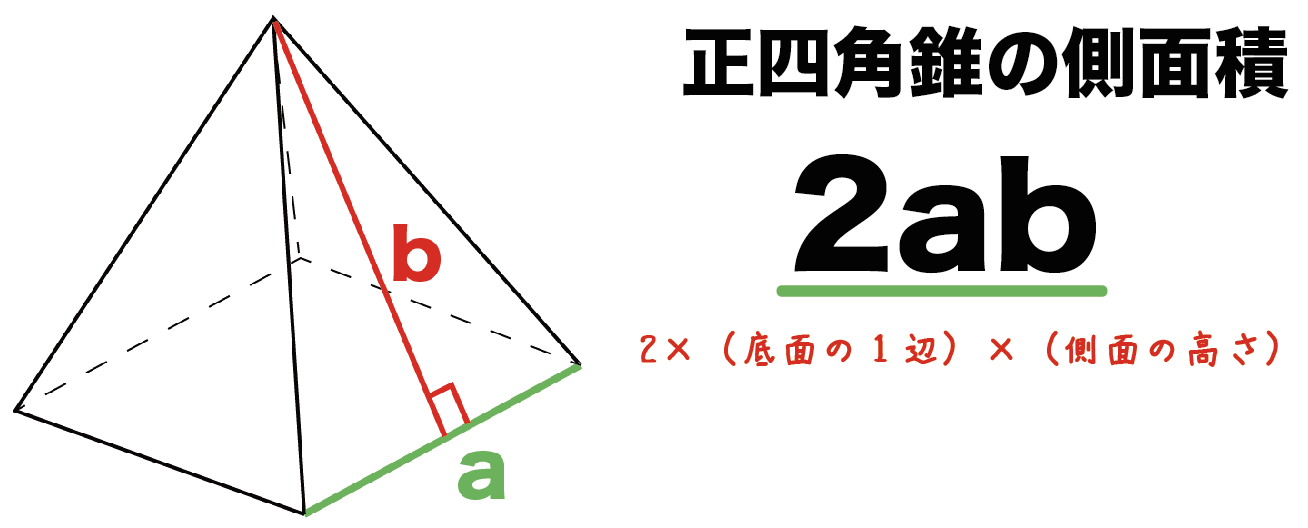



計算公式 正四角錐の側面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
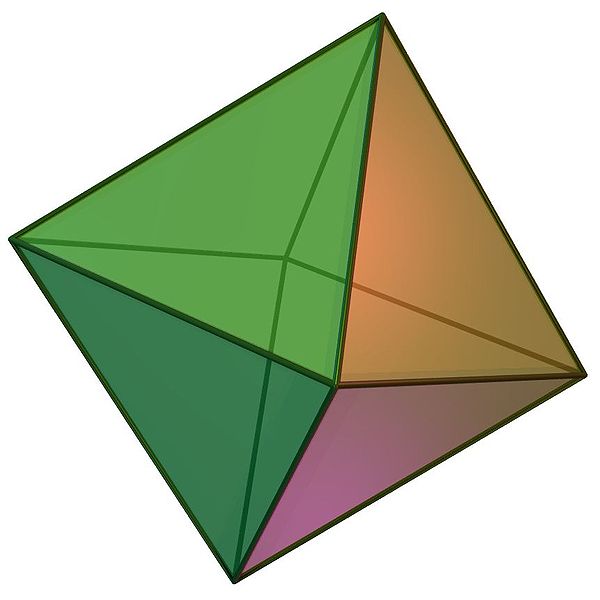



四角錐 分類 詹森多面體 相關多面體 中文百科全書




稜錐 維基百科 自由的百科全書
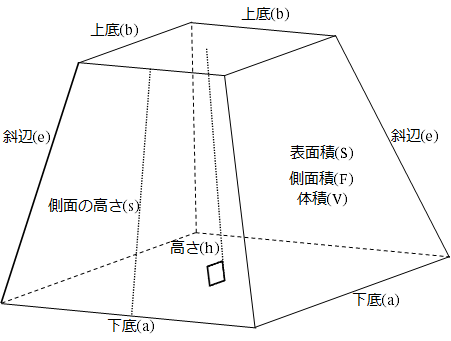



Excelワークシート 正四角錐台の体積や表面積などを計算するワークシート 黒い箱の中




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
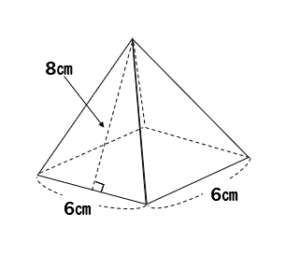



トップ100 正四角錐表面積 最高のぬりえ




五角錐 维基百科 自由的百科全书




1000以上四角錐台体積 ニスヌーピー壁紙



1




高二空間問題四角錐求高四腳錐求體積金字塔求體積求側面與底面的兩面角餘弦空間問題高二下第一章106龍騰課後卷計算題
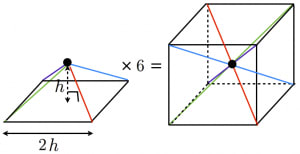



錐体の体積に1 3がつくことの2通りの説明 高校数学の美しい物語



図は側面が正三角形の正四角錐である 一辺の長さは6 である 1 体積を求 Yahoo 知恵袋



正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学



2



0 件のコメント:
コメントを投稿