1526 Hipotenüs Uzunluğu 108,1666 birim Komşu Kenar Uzunluğu 90 birim Karşı Kenar Uzunluğu 60,0001 birim Yukarıdaki ölçüleri bildiğimizi varsayalım Aşağıdaki α ve β açısının matematiksel hesaplama formülü nedir bununla alakalı bir bilgi paylaşılmamış α açısının ölçüsü 33,6901 derece β Dik açılı üçgen nedir komponon dik açılı üçgen nedir Cevap Dik açılı üçgen nedir Deli Sevdam Dik Üçgen Nedir ve Özellikleri (Geometrik Cisimlerin Özellikleri) Dik üçgen, iç açılarından biri 90° olan üçgendir Çemberde çapı gören çevre açı 90°'dir Pisagor Teoremi Pisagor teoremi, herhangi bir dik üçgende kenarlar arasındaki bağıntıya verilen addırKÜME EĞİTİMBUTİK DERSANE ANKARAİLKER ÇORSUZ

Dik Aci Ucgen Formulleri
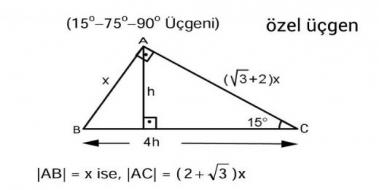
15 75 90 üçgeninin kenar uzunlukları
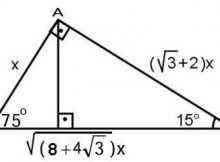
15 75 90 üçgeninin kenar uzunlukları- (30° – 30° – 1°) Üçgeni (30° – 30° – 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgenindeüçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir




Mat Geo Fen Ucgenler Hakkinda Genel Hatirlatmalar 1 Orta Taban
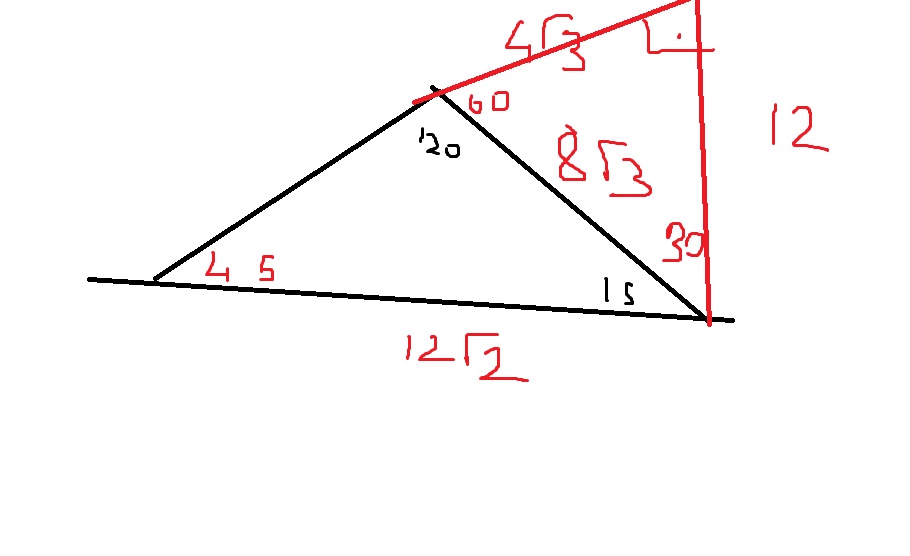
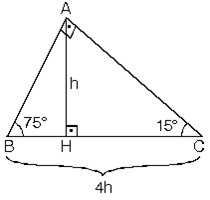
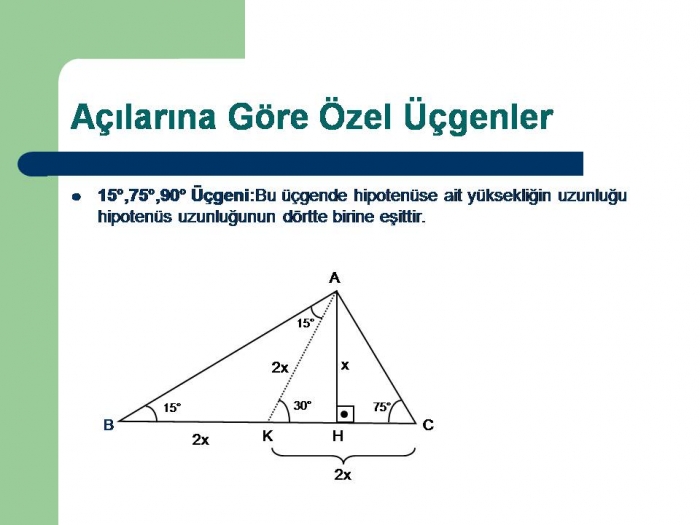
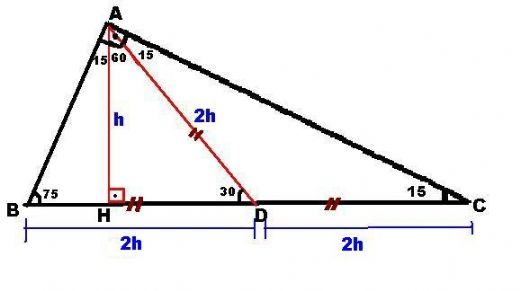
Üçgeni Kenar Bağıntısı ( İSPAT ) ABC Üçgeninin Alanı = 1/24x4xsin30 olmak üzere 4x²dir ADC Üçgeninin alanı da bunun yarısı 2x²'dir 15 75 90 üçgeninde 15 derecelik açının karşısında ki kenar 1cm olarak düşünülür ise 75 derecelik açının karşısında ki kenar 2kök 3 olmaktadır Ayrıca hipotenüse indirilen dikme 1 cm iken indirilen kenar 4 cm olmaktadır5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur
Bu yazıda 15 75 90 üçgeni kenar bağıntıları ve özellikleri üzerinde kısaca durmaya çalışacağız Geometri dersinde özel üçgenleri iyi bildiğimiz zaman geri kalan üçgenleri de bu üçgenlere benzeterek soruları çözme yoluna gideriz Daha önce 30 60 90 üçgeni yazısında başka bir temel üçgenin özelliklerinden bahsettik Eğer kuralını bilmiyorsanız mutlaka 30 60 90 üçgeni özellikleriniDiküçgeninin kenarları üzerindedir 75 8 15 x 16 8 15 x 16 a (30 60 90) üçgeni ve ECD üçgeni de (0) üçgeni olur ABC eúkenar üçgeninin bir kenar uzunluğu 12 cm olduğundan EC = 4 cm dir AFE dik üçgeninde 90 yi gören AE = 8 cm ise5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur
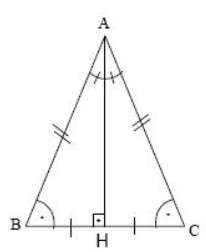
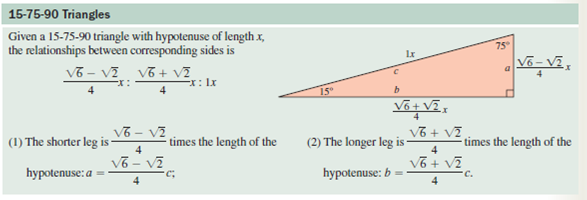
üçgeninin kenarları arasındaki oranların ispatını öğrenin üçgeninin kenarları arasındaki oranların ispatını öğrenin If you're seeing this message, it means we're having trouble loading external resources on our website Üçgeni Kenar Oranları İspatıBir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdır şekilde, m(A) = 90° BC kenarı hipotenüs AB ve AC kenarları dik kenarlardırVeya üçgeni gördüğünüzde bu orana göre, biraz önce gördüğümüz oranlara göre kenar uzunluklarını bulabilirsiniz Mesela kenarları 2, 2 kök 3 ve 4 olan bir üçgen gördünüz 2'nin 2 kök 3'e oranı, 1 bölü kök 3 2'nin 4'e oranı da 1 bölü 2'dir Dolayısıyla bu üçgen üçgenidir




15 75 90 Ucgeni Pow Bylge




45 45 90 Ucgeni Kurali Nedir 45 45 90 Ucgeninin Ozellikleri Nelerdir Habertos
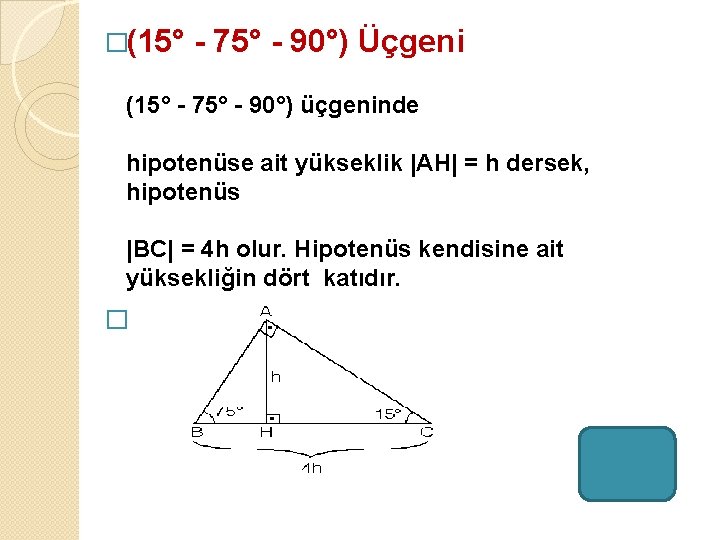
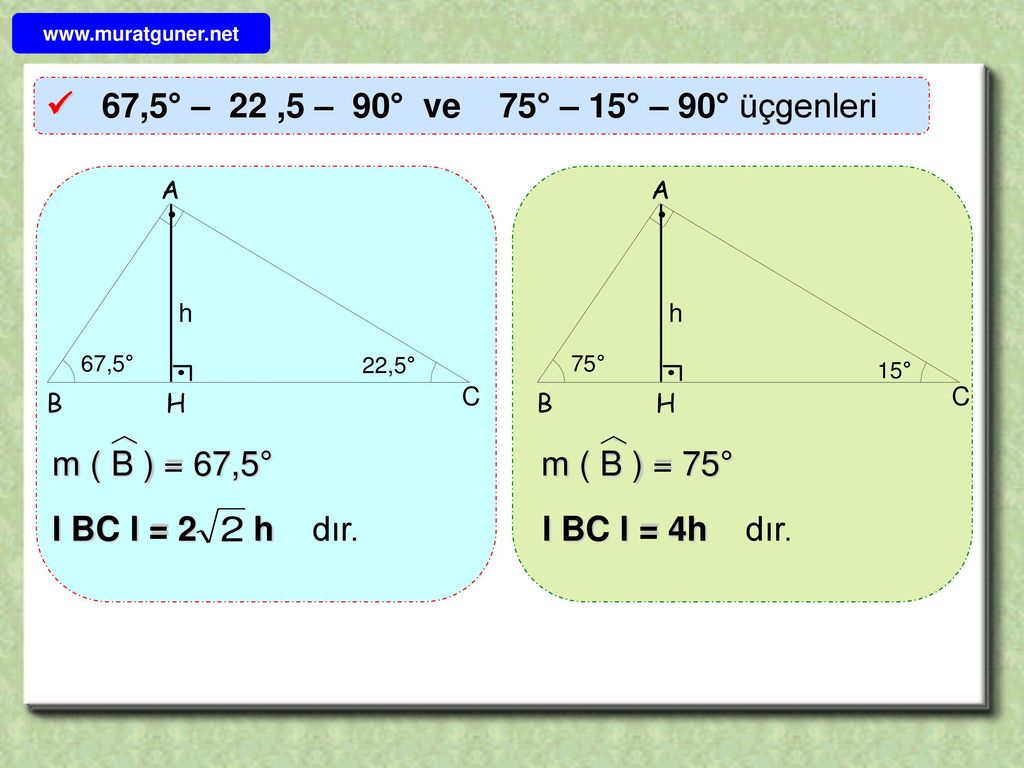
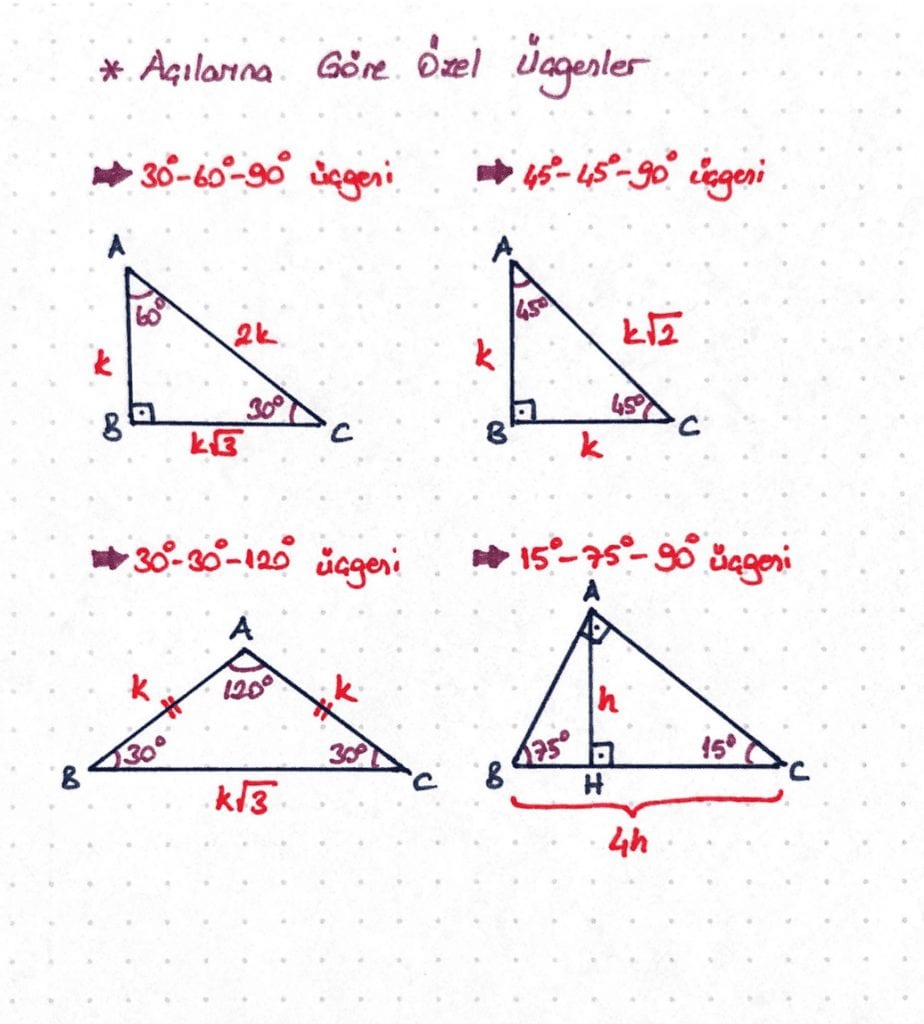
(15 75 90) Üçgeni (45 45 90) Üçgeni; (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdır (15°, 75°, 90°) dik üçgeninde hipotenüsü ait yükseklik hipotenüsün dörtte birine eşittir 30 30 1 Üçgeni 30 – 30 – 1 ikizkenar üçgeni iki adet 30 – 60 – 90 dik üçgeninden oluşur 1 0 'nin karşısındaki kenar ikiz kenarların √3 katına eşittir




Ozel Ucgenler Nelerdir Ozel Ucgenler 8 15 17 7 24 25 30 60 90 Ve Diger



15 75 90 Ucgeni
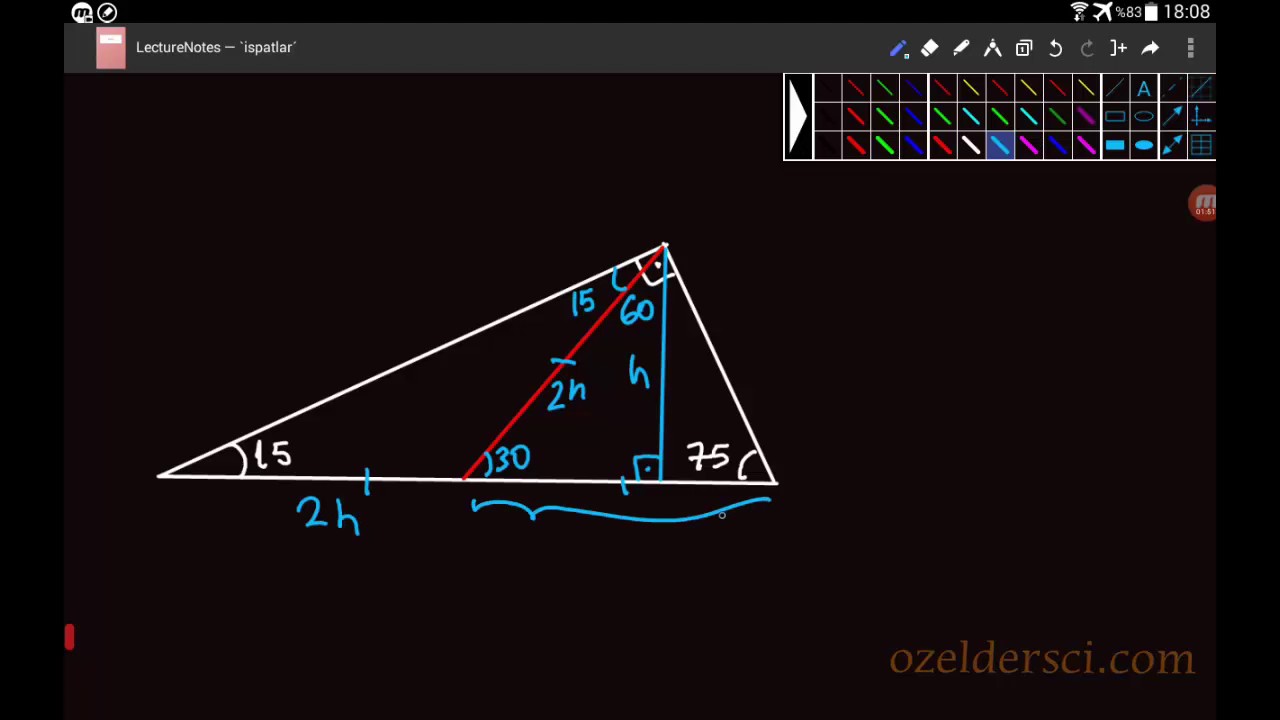
Üçgeni (h4h) İSPAT üçgeninde hipotenüse indirilen yüksekliğe h diyelim Daha Sonra Süper üçlüyü kullanmak için hipotenüsü iki eşit parçaya bölecek kenarortayı çizelim 3 adet üçgenimiz oluştu () () (0) 30⁰'nin karşısına h dediğimiz zaman 90⁰'nin karşısına 2h 14 Özel dik üçgenler üçgeni Bu üçgende 15°lik açının karsısındaki kenar 1 cm ise 75°lik kenarın karsısındaki kenar 2 3 {\displaystyle 2{\sqrt {3}}} cm olur Ispatı ise üçgenindeki gibidir Tek farkı, 75°lik açının 15° ve 60°lik açılara bölünmesidirX 2 cm buluruz 11




Dik Ucgen Vikipedi



Ozel Ucgenler Not Bu
üçgeni Bu üçgende 15 derecenin gördüğü kenar 1 cm ise 75 derecenin gördüğü kenar 2kök 3 cm uzunluğundadır Kenara göre Kenara göre özel üçgenler aslında işlem yapmadan pratik olarak akılda tutulması için ortaya çıkmıştır5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur(30 60 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz Sizi ve arkadaşlarınızı sitemize bekliyoruz ) Tüm Öğrencilerimize İyi Dersler Diliyoruz )



15 75 90 Ucgeni Ozelliklerinin Ispati Youtube




Mat Geo Fen Ucgenler Hakkinda Genel Hatirlatmalar 1 Orta Taban
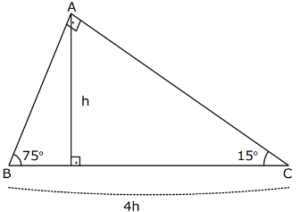
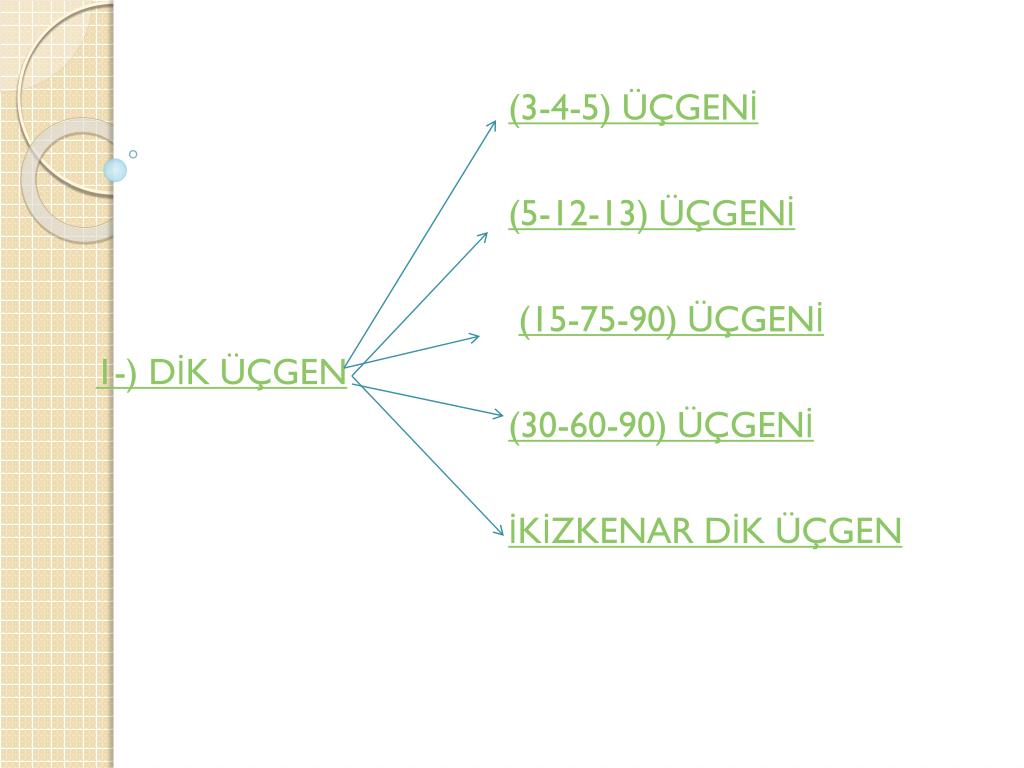
özel bir dik üçgendir 90 derecelik açının karşısında hipotenüs bunulunur Bu 90 derecelik açının olduğu yerden hipotenüse indirilecek dik (yani yükseklik) h olursa hipotenüs de 4h olacaktır 5 ayrıca 75 ten uzatılacak kol ile 15 15 eş üçgeni ve 30 60 90 dik üçgeniÜçgeni Kenar uzunlukları (3 – 4 – 5) sayıları veya bunların katı olan bütün üçgenler dik üçgendir (6 – 8 – 10), (9 – 12 – 15), gibiBu bakımdan kenar bağlantılarını bilmek üçgenin tanımının da yapılmasını sağlayacaktır 15 75 90 üçgeni içinde 90 dereceden hipotenüs kısmına kadar indirilmiş olan bir dikmenin uzunluğu hipotenüsün 4'te biri kadar olmaktadır




Geometri 7 15 75 90 Ucgenleri Bolum 2 Youtube




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim
リコーダー運指表 全音楽譜出版社 ドレミファソラシドだけで演奏できる曲の楽譜 全音楽譜出版社 小学生のための歌とソプラノ リコーダーで奏でる すぐ使える無料楽譜 スタジオジブリ 天空の城ラピュタ 全4曲 ピアノ塾 山のポルカ 小学生の音楽3 より7 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar a 3 olur 8 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur 15 75 90 Üçgeni (15°, 75°, 90°) dik üçgeninde hipotenüsü ait yükseklik hipotenüsün dörtte birine eşittir 30 30 1 Üçgeni 30 – 30 – 1 ikizkenar üçgeni iki adet 30 – 60 – 90 dik üçgeninden oluşur 1 0 'nin karşısındaki kenar ikiz kenarların √3 katına eşittir Dik Üçgen ve Öklid Kuralları



15 75 90 Ucgeni




Net Fikir Acilarina Gore Ozel Dik Ucgenler
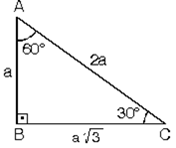
5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur60 derecenin karşısındaki kenar 30 derecenin karşısındaki kenarın kök 3 katıdır, hipotenüs kenarıda 30 derecelik açının iki katıdır Üçgeni; üçgeni şükela tümü bugün hic sevmedigim ucgen, yukseklik teoreminden baska ise yarar bir seyi de yok, kose bagintilari tamamen gereksiz, cek kardesim cizgileri bak nasil cikiyor ikiz kenar ucgenler ordan cikiyor kenarlar




Dik Ucgen 6 15 75 90 Ucgeni Geometri Metin Hocam Youtube




15 75 90 Ucgeni Ozellikleri
üçgeni değiştir kaynağı değiştir Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir(15 75 90) Üçgeni (15 75 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz BC kenarı hipotenüstür ve m(A) = 90° dir 15° 75° 90° üçgeni özel dik üçgen sınıfında yer alır m(A) = 90° olduğuna göre A köşesinden BC kenarına ait bir dikme ile yükseklik çizilir Bu yükseklik h ile gösterilirken BC kenarında H noktası ile işaretlenir




Ozel Ucgenler Konu Anlatimi Ogretmen Tercihim
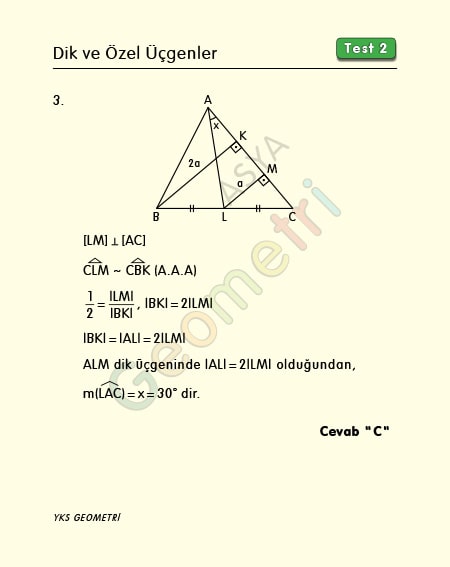



Dik Ve Ozel Ucgenler Test 2
A) 3 B) 2 C) 2 2 D) 2 3 E) 4 Çözüm 135 'lik açının olduğu yerden, dışarıya doğru bir dik üçgen oluşturursak 45 – 45 – 90 üçgeni oluşur Bu üçgenin kenarları 6'şar cm olur Büyük üçgen de 6 8 10 üçgeni olduğundan;15 75 90 Üçgeni kuralı geometri dersinde özel üçgenler konusu adında yer alır Diğer özel üçgenler kadar yoğun bir şekilde soru öbekleri bulunmasa da çıkabilecek az sayıdaki sorularda ayırt edici problem şeklinde kendisini belli öder15 75 90 Üçgeni Geometri dersi için önemli özel üçgenlerden olan 15 75 90 üçgeni üçgenin sabit oranından gelmektedir Dik üçgen 15 75 90 üçgen özelliği ve 15 75 90 üçgeninin 2 pratik kuralı ve örnek çözümlü sorularPratik Geometri Yöntemleri videolarımda sizlere mantık ve pratik yönte
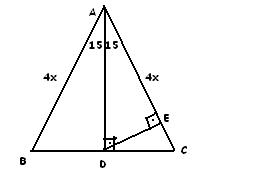



15 75 90 Ucgeni Kenar Bagintisi Ispat
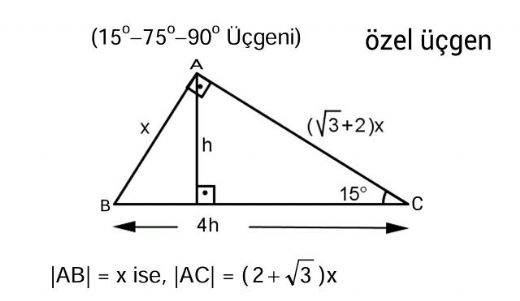



90 75 15 Ucgeni Ozellikleri
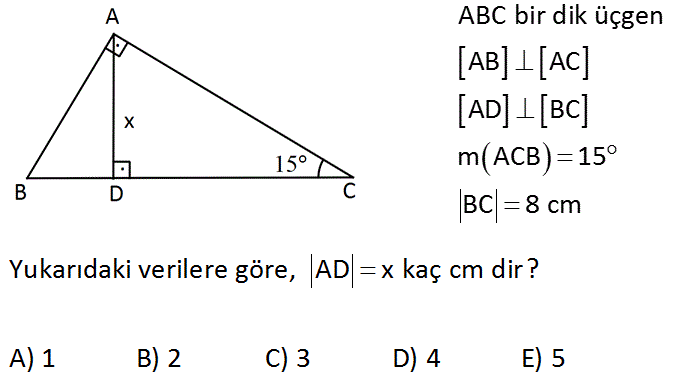
Soru Sor sayfası kullanılarak Özel Üçgenler konusu altında üçgeni ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz 1575 90 Üçgeni Bu üçgende hipotenüsün yüksekliğine x dediğimiz zaman hipotenüsün uzunluğu bu ölçünün 4 katı yanı 4x olmaktadır İkizkenar Üçgen Özellikleri 新しい 小学 5 年生 算数 割合 文章 問題 小学5年生の算数 百分率と歩合割合の表し方 練習問題プリント 教材の新学習指導要領への対応について ただいまちびむすドリル小学生では公開中の教材の 新学習指導要領年度スタートへの対応 を進めております




Daha Fazlasi Icin Takip Etmeyi Unutmayin Yks Ayt Ayt21 Tyt Tyt Tyt21 Kpss Kpss 21 Ayrik Matematik Ders Programlari Ders Calisma Ipuclari




Ucgenlerde Uzunluk Matematik Ve Geometri
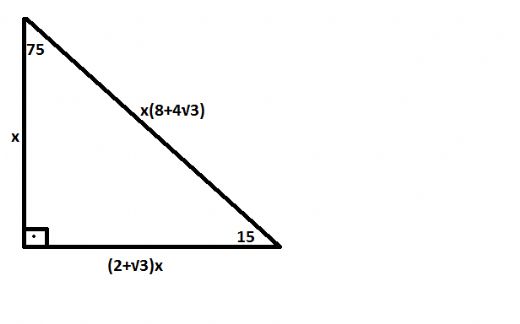
Dik açının karşısındaki kenar hipotenüse çekilen yüksekliğin (öklid bağıntısının) 4 katıdır Yukarıdaki 15 75 90 üçgeninde verilen kenar oranları bu üçgeni anlamamız için önemli oranlardır Yukarıda da dediğimiz gibi bunları ezberlemek zorunda değilsiniz ancak bilirseniz size zarar değil fayda sağlar 15 75 90 üçgeni bir dik üçgen olduğu için bu konuya çalışmanızı öneririz Pisagor teorimi ve dik üçgen ile ilgili özellikler burada da aynen geçerlidir 15 75 90 ÜçgenininÇözüm Pisagor bağıntısında 9 12 15 üçgeni diye bir özel üçgen olduğunu biliyoruz Öyleyse burada da B açısı 90 derece olsaydı x 15 olacaktı Ancak bu açı 90 dereceden büyük olduğu için x de 15'den büyük olacaktır




Ozel Ucgenler Nelerdir Acilarina Ve Kenarlarina Gore Ozel Ucgenler Konu Anlatimi
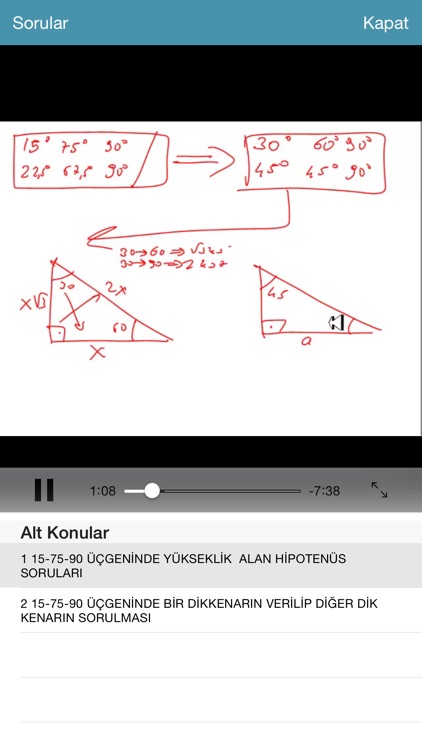



15 75 90 Ucgeni
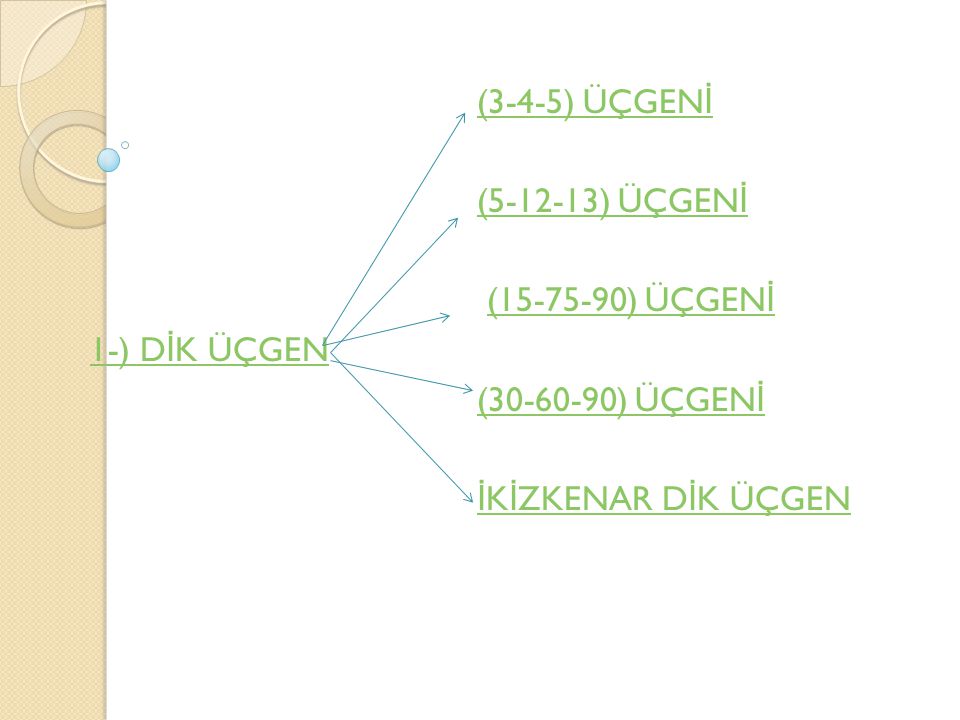
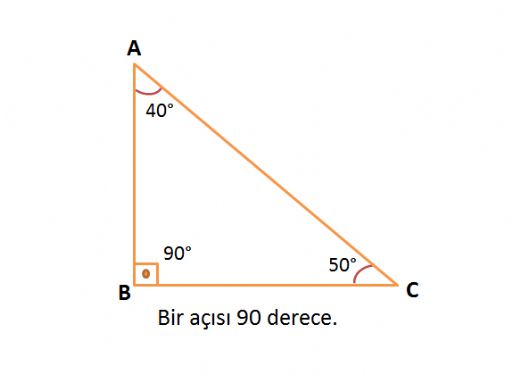
Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdır şekilde, m(A) = 90° BC kenarı hipotenüs AB ve AC kenarlarıDİK ÜÇGEN 16 15 75 90 ÜÇGENİ kaydeden Mustafa YAZAGAN 65 Matematik Science Sigmund Freud Brent Rivera Daha fazla bilgi Bunun gibi daha fazlasıBu dik üçgende kenar uzunlukları için Pisagor teoremi uygulanmaktadır 15 75 90 üçgeninin en önemli özelliği ise 90 derecelik açıdan indirilen yüksekliğin hipotenüs yani 90 15 75 90 üçgeni özellikleri Bir dik üçgendir İki dar açısının toplamı dik açısını vermektedir İki dar açı karşısındaki dar kenarlarının toplamı her daim dik açının karşısındaki geniş kenar uzunluğunu vermek zorundadır




30 60 90 Ucgeni Ve Ozellikleri Not Bu



1000以上 75 15 90 Ucgeni Kenarlari
üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu üçgende hipotenüse indirilen dikme, hipotenüsün katıdır 15 75 90 üçgeni Genellikle geometri dersinde çok daha fazla karşılaştığımız bir özel üçgendir öğrenciler okul hayatları boyunca çeşitli yaşlarda ve sınıflarda bir çok sınava tabi tutulur Bu sınavlar sonucunda yetenek ve ilgi alanları, başarı olduğu dersler ve başarı boyutları belirlenir



Ozel Ucgenler Nelerdir Acilarina Ve Kenarlarina Gore Ozel Ucgenlerin Ozellikleri Egitim Haberleri




Ispat 15 75 90 Ucgeni Tyt Geometri Ozel Ucgenler Youtube




Dik Aci Ucgen Formulleri




15 75 90 Ucgeni Akilli Geometri




Dik Ucgen Wikiwand




En Hizli 30 60 90 Ucgeni Kenar Hesaplama



Dik Acili Ucgen Kenarlarina Gore Ucgenler




15 75 90 Ucgeni Ozelligi



Dik Ve Ozel Ucgenler 1




Dik Ucgen 17 22 5 67 5 90 Ucgeni Ders Calisma Ipuclari Evde Egitim Egitim




En Hizli 30 60 90 Ucgeni




Geometri 15 75 90 Ucgeni Nasil Olur Youtube



30 60 90 Ucgeni Kenar Ozellikleri




15 75 90 Ucgeni Not Bu
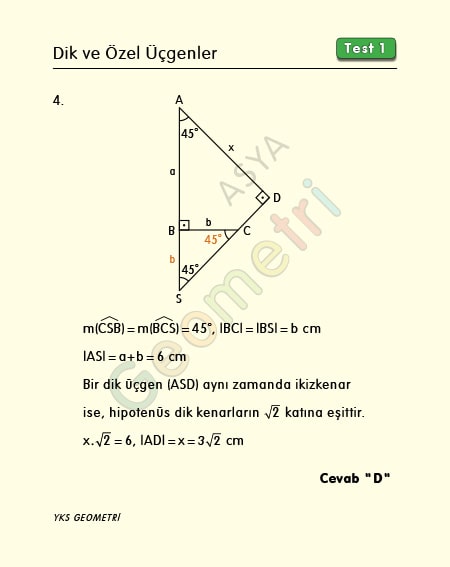



Dik Ve Ozel Ucgenler Test 1
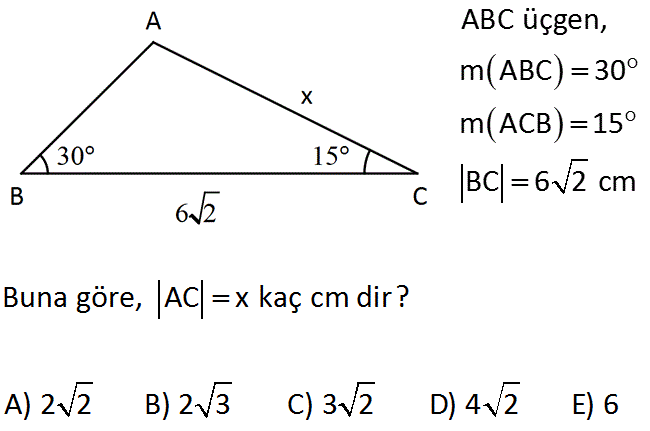



45 45 90 Ucgeni Ikizkenar Dik Ucgen




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz
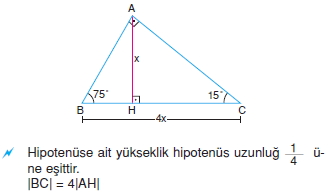



Ozellik 5 Bilgicik Com Bilgicik Com




Dik Ucgen 15 75 90 Ucgeni Islemli Em Iyi Secicem Gereksiz Engellenir Eodev Com
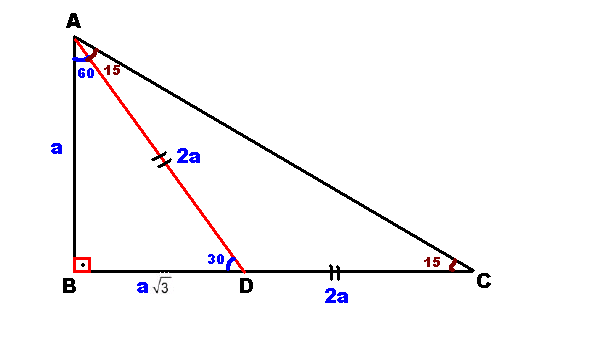



15 75 90 Ucgeni 2 3 Ispat



Populer Icerik



印刷可能 75 15 Ucgeni シモネタ




75 15 90 Ucgeni Kenarlari シモネタ




Ozel Ucgenler Diyot Net Nedir




Dik Ve Ozel Ucgenler



Ozel Ucgenler




Genler Gen Etler Ekenar Gen Kzkenar Gen Dk



1




Murat En Akdenz Nverstes Ge Nler 1



1




15 75 90 Ucgeni Kelime Detayi




15 75 90 Ucgeni Ozellikleri Ve Kurallari




45 45 90 Ucgeni Ozellikleri



1



Dik Ve Ozel Ucgenler 1




Dik Ucgen Vikipedi




Ozel Ucgenler



Ozel Ucgenler Konu Anlatimi




135 30 15 Ucgenini Aciklayabilir Misiniz Eodev Com



45 45 90 Ucgeni Matematikce




15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List



1




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Egitim Haberleri




Image Selectionnee 75 15 Ucgeni



15 75 90 Ucgeni Uludag Sozluk




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali




lurplvgm7frm




Dik Ucgen 16 15 75 90 Ucgeni Matematik Felsefesi Temel Matematik Evde Egitim




Ozel Ucgenler Konu Anlatimi Ogretmen Tercihim



Zel Genler 1 Dk Gen 2 Kzkenar Gen




Ozel Ucgenler



100以上 75 15 90 Ucgeni Ozelligi シモネタ



Ppt Ozel Ucgenler Powerpoint Presentation Free Download Id




15 75 90 Ucgeni Webders Net



Bit Ly 3nxrbx4




lurplvgm7frm



最新 75 15 90 Ucgeni シモネタ




45 45 90 Ucgeni Nedir Ozellikleri Nelerdir Nasil Hesaplanir En Son Haberler Milliyet




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube
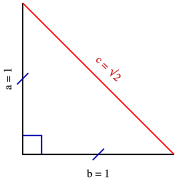



Dik Ucgen Vikipedi
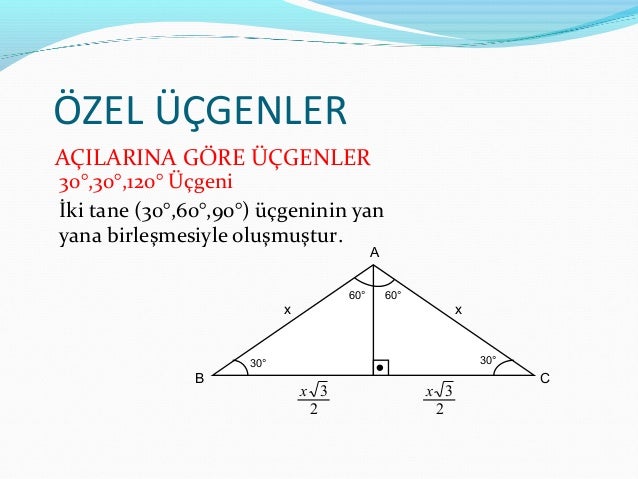



Ozel Ucgenler




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali




45 45 90 Ucgeni Kenar Oranlari Video Khan Academy




Geometri 7 15 75 90 Ucgenleri Bolum 1 Youtube
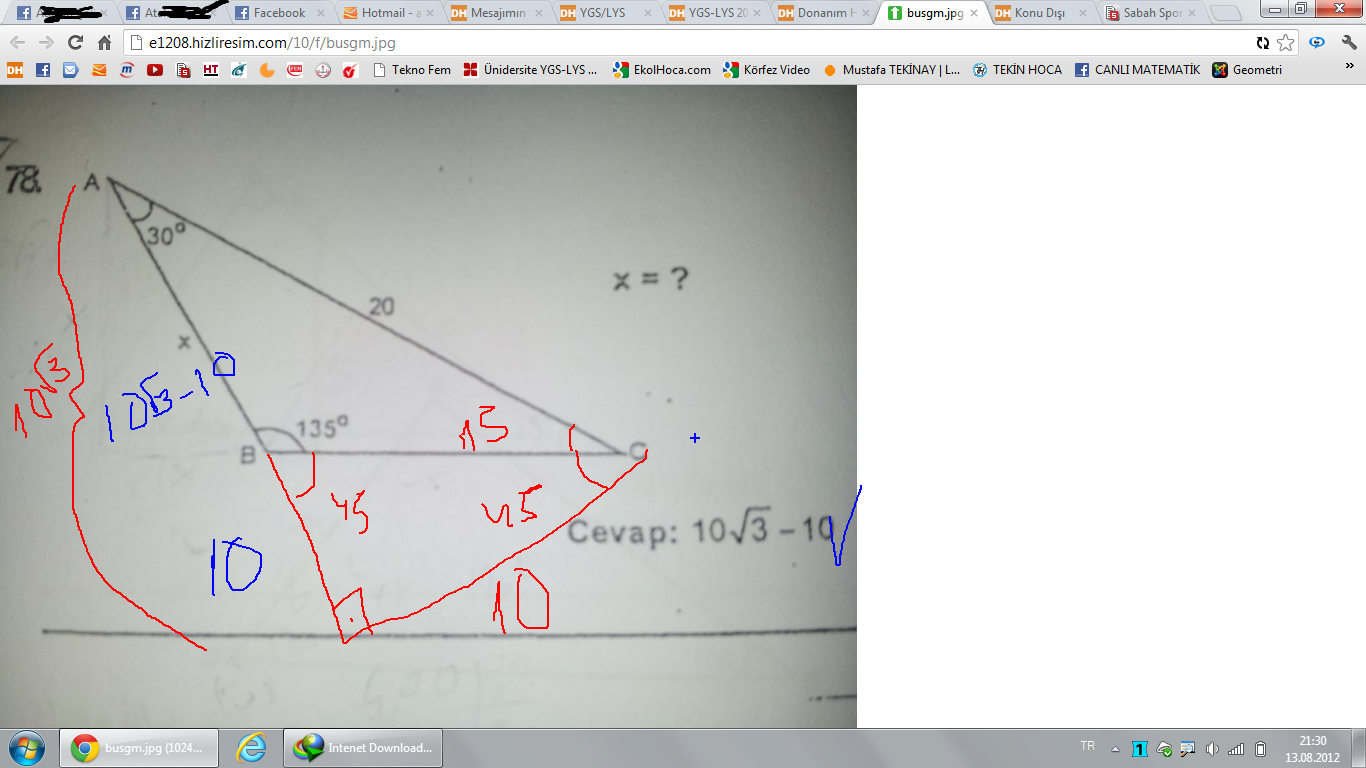



15 75 90 Ucgeni




15 75 90




15 75 90 Ucgeninde H 4h Kuralinin Ispati Youtube
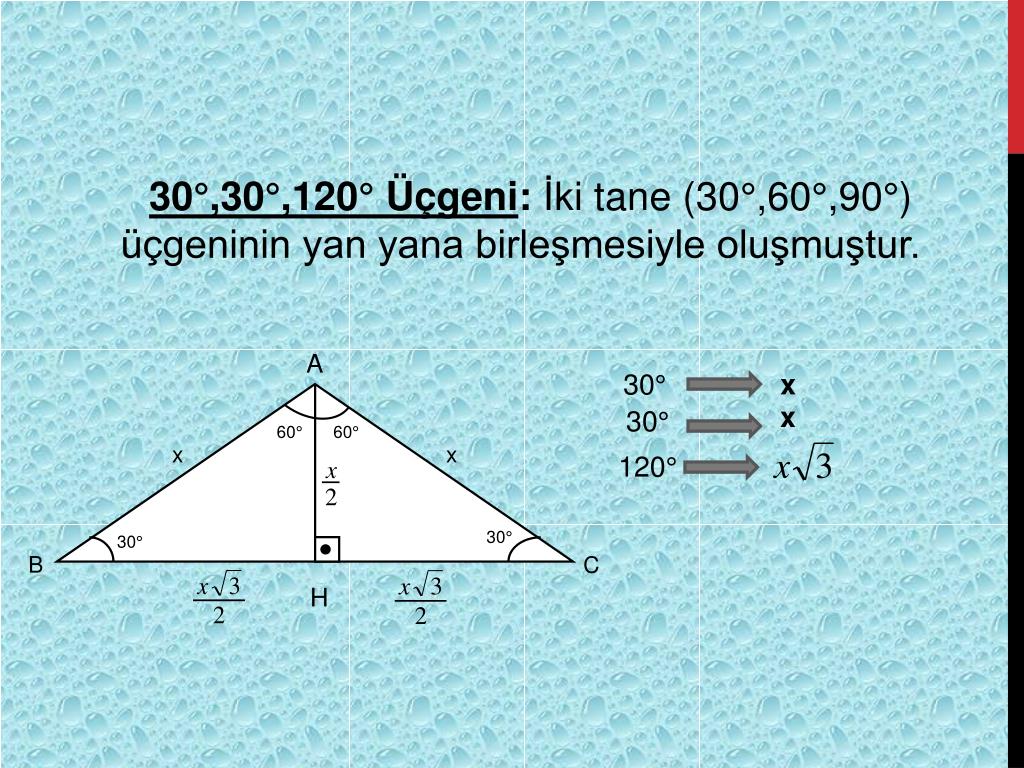



Ppt Ozel Ucgenler Powerpoint Presentation Free Download Id




lurplvgm7frm




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz



15 75 90 Ucgeni Ozellikleri




Dik Ucgende Trigonometri




16 Ozel Ucgenler



Matematik Ogrenebilir Ppt Indir




3 4 5 Ucgeni Ve Ozellikleri Not Bu



30 60 90 Ucgeni Kenar Oranlari Ispati Geometri Khan Academy Turkce




45 45 90 Ucgeni Ozellikleri



15 75 90 Ucgeninin Ozellikleri Nelerdir



15 75 90 Ucgeni Cozumlu Sorular



0 件のコメント:
コメントを投稿